In 1949 Claude Shannon (and some of his pals) came up with a pretty clever framework for how information can be transmitted over an arbitrary channel in the presence of noise. A channel simply refers to any medium where a signal can be modulated. Information refers to knowledge not previously available to the reciever. If I tell you I’m going to say 1, and then I say 1, no information has been transferred, it must be new knowledge, which is important when we think about encoding information.

So who cares? Well all of modern society is built on this premise of information theory. So everyone cares. Netflix, the internet, iMessgage (shilling so everyone has blue messages), and every other form of media consumed today are all built on the principles laid down by Shannon. So it’s a quite important topic.

When we consider information flow really the first problem that comes to mind is speed. How fast can we go and still recieve the original, sent, data? What is the absolute maximum amount of information can we send in the presence of noise? The answer is spectacularly simple and is given by the famous Shannon-Hartley theorem.

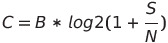
Here C is the channel capacity in bits per second, B is the channel bandwidth in hertz, and S/N gives the signal to noise ratio (SNR) of the channel in linear units (not dB!). Commonly instead of looking at noise power and signal power in absolute units (just watts) we look at a more useful quantity reffered to as Eb/No. Eb is the energy per encoded bit, and No is the noise power spectral density, or the noise power across 1 Hz of bandwidth. This is really just a normalizaton of SNR per bit, not complex at all.

So Shannon has given us the theoretical limit. He must also tell us how to reach that limit right? Funnily enough no. Shannon shows in the proof that if he constructs a random code (where a code is the method of protecting bits against bit flips due to noise), he can make it arbitrarily good, up to the channel capactiy. He does not however, give an exact code. In essence he proves the existence of such codes, but does not provide the code (insert mathematician xkcd here). Thankfully he was likely thinking of providing jobs to future communications engineers, because developing good codes now employs quite a few people!

In this post I’d like to cover how data is encoded in a convolutional encoder, then in the next part cover the decoding, and in the future move on to their more modern cousin, turbo codes. The whole idea of an encoder/decoder pair is to attach some redundant information at the encoder, so the decoder can figure out what the original message was, even if many bits have flipped. We can then ignore channel noise, and thus send information more efficiently.

So say you’re streaming a live video from ESPN on your desktop. Your processor is recieving data over your ethernet connection, then parsing that data, then painting the pixels on your monitor as the data tells it they shoud painted (obviously a simplistic view but bear with me). In transmission a lightening strike could occur, causing a surge somewhere along the line, injecting energy into the system, and flipping bits. You will see this on the screen, some character will briefly have a green head or something. That is annoying. So how do we defend against this?

We could encode blocks of information using things like Hamming codes or BCH codes, called linear block codes, but ESPN is a streaming service, and encoding blocks of information doesn’t allow one to easily jump into a stream since we have to encode large blocks to get a decent code. Here is where the idea of convolutional encoding comes in. We pass a data stream, just pure 1’s and 0’s, into our encoder block, with no delay, then send an encoded data stream out into the channel. The decoder receives this stream, and then decides how to decode that original data. This is all done continuously, there is no block delay here in this pure convolutional system (realistically we combine this technique with a linear block code for best performance).

Ok so the idea is simple, how do we actually do it? It’s really an extremely simple circuit that makes use only of delay elements and XOR’s, and really all we’re doing is building a digital filter. The image below should give a basic idea of the circuit. (The example I give is from wikipedia so I don’t have to draw the trellis in the decoder, for a more formal explanation visit https://en.wikipedia.org/wiki/Convolutional_code)

Here D1 is the LSB, D3 is the MSB, and D1-D3 represent D flip flops, simply holding one logic value, 0 or 1. The XOR operation can be seen as well. The output for every clock cycle (the system is clocked to bring in data) is {S1,S2,S3} so input is one message bit m, the clock cycle hits, D3 takes the value from D2, D2 gets D1’s previous values, and D1 takes the new message bit. The new output value is then computed and sent out over the channel. Easy! The hard part comes when we want to figure out the message that was originally sent, which I’ll cover in the second part of this post.