The previous post hopefully lent some intuition behind the Hilbert transform, and ideally this post will extend that intuition to photonic implementations of the algorithm.

The first thing to note is that any physical device that creates a Hilbert transform will introduce some distortion and loss. This is due to the fact that the the ideal Hilbert transform is NOT causal, ie for t<0, H(x(t))!=0. This implies that a Hilbert transformer must be a bandpass filter that mostly preserves amplitude, and offers a pi/2 phase shift.

Thankfully optical phase shift really isn’t that hard! The initial way people did this was just by mixing and matching materials (ie a lens or a plate) until the saw the phase shift in light they wanted at the output. This generally sucks though, lots of diffraction, lots of loss, etc.

People moved on from free space implementations pretty quickly. When light travels through a fiber it’s generally much easier to manipulate. A decent recent example of a photonic Hilbert transformer can be seen here

The first thing to notice is one must first filter the signal. The Hilbert transform is ill defined for very broadband signals, phase information very quickly stops making sense if your signal is broadband (Video why). After filtering the authors make use of a Fiber Bragg Grating (FBG) to carry out the actual Hilbert transform. All the result really boils down to is designing the appropriate FBG to give the correct phase/amplitude response. The authors go into how they did that (computationally) in the paper.

The only real thing to realize is this: if you can build a filter with a response that at least somewhat resembles the image below, you can compute a Hilbert Transform about some angular frequency.

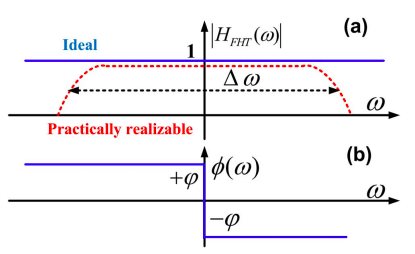
After computing the Hilbert transform we can do all the fun things we did before, one can choose to transduce the signal to the electrical domain and sample it into a processor (say to compute the analytic function of your input signal), or continue processing the signal in the optical domain.